Représentation d'une trompette de Gabriel
(Auteur J.L. BIAGGI)
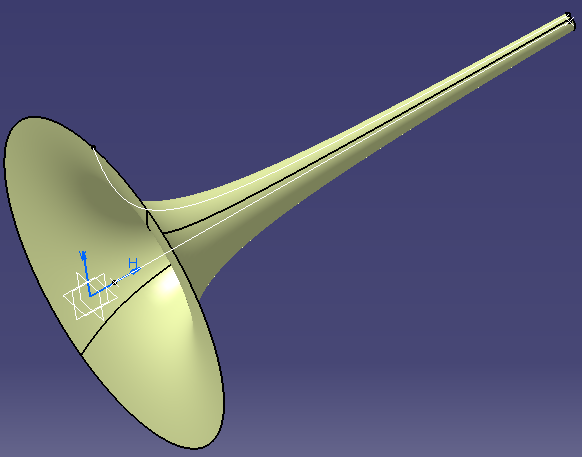
Dans cette activité vous allez représenter une trompette de Gabriel ce qui sera l'occasion d'utiliser le solveur d'équation intégré à Catia, et de mettre en oeuvre la fonction loi qui permet entre autre de représenter dans l'espace une courbe dont l'équation est connue.
- Utilisation de Catia pour la résolution d'un système d'équations
Dans cette première partie, nous allons mettre en oeuvre le solveur de catia intégré à catia pour déterminer les paramètres caractéristiques de l'hyperbole équilatère.
Travail à réaliser:
- Créez trois paramètres de réels (Real) nommés respectivement:
x1
x2
a
Pour les moment les valeurs de ces trois paramètres n'ont pas d'importance.
- Passez dans l'atelier Knowledge Advisor si vous n'y êtes pas déjà.
- Créez un nouveau systèmes d'équations et saisissez ces trois équations:
x2-x1==800;
x1*100==a*a;
x2*5==a*a
La syntaxe doit être exacte.
Le symbole == signifiant strictement égal.
Les équations doivent être séparées par des points virgule.
Identifiez les paramètres inconnus
Effectuez la résolution des équations et validez.
Remarque: vous pouvez voir une fonction représentant le système d'équation apparaître dans l'arbre de construction.
- Définition d'une loi et utilisation pour générer une hyperbole équilatère
Dans cette partie vous allez créer l'hyperbole équilatère à partir d'une fonction loi utilisant les paramètres dont on atrouvé les valeurs avec le système d'équation.
Travail à réaliser:
- Passez dans l'atelier surfacique (Generative Shape Design).
- Activez le plan XY comme support de travail (Outils > Grille > Travail sur support )
- Sur ce support de travail, créer un premier point, Point.1, aux coordonnées égales à:
Remarque:le paramètre x1 étant un réel sans unité, on le multiplie par 1mm pour que le résultat soit homogène à une longueur.
- Puis un second point, Point.2, à:
- Tracez une ligne joignant les deux points.
- Créez une nouvelle Loi. puis pour définir la loi, créez deux nouveaux paramètres formels de type réel, R et Pa, enfin saisissez la loi correspondant à l'équation de l'hyperbole équilatère:
R=5*x2/(Pa*(x2-x1)+x1)
- Créez la courbe parallèle à la droite en utilisant la loi comme définition de la transformation.
Vous pourrez remarquer que le paramètre Pa varie entre 0 et 1.
- Passez le support de travail en mode non actif.
- Réalisez la révolution surfacique sur 360° de la courbe obtenue , on prendra comme axe la droite construite précédemment.
- Dans l'atelier Part Design, créez un volume en épaississant de 1mm la surface, on l'épaissira vers l'extérieur.
- Introduction de paramètres constants dans le système d'équation
Nous allons maintenant introduire des paramètres constants dans notre système d'équations. Nous allons voir que si on modifie un de ces paramètres, la résolution du système d'équation et la géométrie seront de suite mis à jour en conséquence.
Travail à réaliser:
- Créez trois nouveaux paramètres réels:
- Editez le set d'équations préalablement créez, dans les équations existantes, remplacez:
- 800 par L
- 100 par y1
- 5 par y2
Vous devriez alors avoir ce système d'équations:
x2-x1==L;
x1*y1==a*a;
x2*y2==a*a
Ne fermez pas encore la fenêtre.
- Faites le bilan des paramètres inconnus, puis donnez aux paramètres L, y1 et y2 un statut de paramètres constants.
Ne fermez pas encore la fenêtre.
- Donnez à ces trois paramètres constants les valeurs suivantes:
Fermez la fenêtre en cliquant sur OK.
- Dans la loi qui défini le profil de la trompette, remplassez aussi 5 par y2.
- modifiez la valeur du paramètres y1 à 300 et observez les modifications de la géométrie et des valeurs des autres paramètres.
- Réinvestissement - réalisation d'une poutre circulaire à surface de section évoluant linéairement.
Créez une poutre ayant ces caractéristiques:
Félicitations, vous avez terminé le travail.

