Dans cette exercice nous allons revenir sur la modélisation discrétisée de barre métallique mais cette fois en spécifiant des propriétés du matériau en fonction de la température et en ajoutant un échauffement par unité de volume (comme pourrait créer un courant électrique par effet Joule).

 On considère un milieu homogène, limité par les plans x = 0 et x = L avec une surface de section droite unité. Le matériau est de l'alumine dont la conductivité thermique varie avec la température suivant la loi :

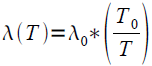
Pour cette partie, on découpera le matériau en 5 masses égales.

Données:

• la barre à une longueur de L=10 centimètre et une section de 1m²
• Mise à part à ses extrémités, n'échange pas de chaleur avec l'extérieur
• à T0=1000K, la conductivité thermique du matériau vaut 8.5 W/(m.K)
• les températures aux extrémités de la barre valent respectivement T1=600K et T2=1200K
• la température de fusion du matériau vaut T=2100K=1827°C
• la masse volumique du matériau vaut 3,97g/cm3
• Cp=0,753 J/(g.K)

Travail à réaliser:

Pour l'ensemble de l'étude, on ne s'intéressera qu'aux régimes établis de transferts thermiques.

1. Modéliser notre système en choisissant le sous-modèle THSD1 pour représenter les propriétés de l'alumine. Il faudra alors associer ces trois fichiers caractéristiques du matériaux à cette fonction pendant la phase de paramétrage:
   • capacité calorifique: cp.dat
   • Conductivité: k.dat
   • Masse volumique: density.dat
   
   Spécifier pour les propriétés du matériau des interpolations de type cubiques.
   
   Comme il n'est pas possible de tracer directement sous AMESim la température de différents éléments, faites-le avec un logiciel externe (tableur par exemple).
   
   
2. On dispose, à l'intérieur de ce matériau, d'une source de chaleur qui dissipe une puissance volumique P uniforme. Les températures T(0) et T(L) sont fixées.
   
   
   1. Ajouter ces apports de chaleurs dans votre modélisation et déterminer les nouvelles distributions de température dans les cas où P= 1 MW/m³ puis 4 MW/m³.
      On pourra utiliser une fonction de duplication de signal pour simplifier le schéma du système.
      
      
   2. Déterminez la puissance volumique dissipée Pmin à partir de laquelle la température en un point de la barre devient supérieure à la température de la source la plus chaude (T2=1200K). On déterminera cette puissance volumique à 0.1 MW près.
      On peut trouver une méthode pour répondre à cette question en remarquant qu'à partir du moment où la température dans la barre est localement supérieure à la température de la source la plus élevée (T2), le flux thermique change de sens au niveau de cette source.
      On pourra faire un calcul par batch pour approcher la solution.
      
      
   3. Déterminer, à 0.5 MW près, la puissance volumique maximale Pmax que le matériau peut supporter.
      Pour cette question, on se contentera d'estimer la température maximum dans la barre comme étant la température la plus élevée d'un des éléments de masse.

Quelques résultats

• Pour une puissance supérieure ou égale à 1,2 MW/m³ la température passe par un maximum au sein de la barre.
  
  
• A partir de 5MW/m³ la température dépasse localement la température de fusion du matériau.