Nous allons modéliser un cas simple de conduction le long d'une barre métallique.

On souhaite étudier la conduction thermique le long d'une barre d'aluminium. Initialement, la barre est à température de 15°C. On impose une température de 40°C d'un coté de la barre et toutes les autres parois sont supposés adiabatiques.

 Travail à réaliser:

1. Création du système à simuler par insertion et connexion de composants

   Le logiciel AMESim n'est pas conçu pour simuler des évolutions spatiales (une dimension ou plus). Cependant, on se propose de simuler la conduction le long de la barre (1D) en la découpant en un nombre discret d'éléments n.
   
   

   

   
   
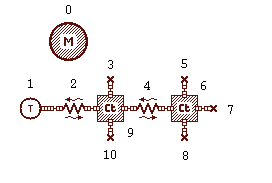
   Réalisez le système représenté ci-dessus où, dans un premier temps, on représente la barre en la découpant en deux tronçons. Vous aurez souci d'identifier clairement le rôle de chacun des composants en utilisant l'aide en ligne.
   
   Remarques: Lorsqu'un composant se trouve plusieurs fois dans un système, l'utilisation du copier (CTRL+C) et du coller (CTRL+V) en série peut s'avérer intéressante.
   
   

2. Choix des sous-modèles physiques à associer à chacun des composants

   Le choix de vos sous-modèles doit permettre:
   
   

   1. de modéliser des transferts conductifs en fonction de la surface d'échange, de la conductivité du matériau, et de l'épaisseur de matière,
      
      
   2. de représenter l'accumulation d'énergie de la matière,
      
      
   3. de modéliser l'apport de chaleur par une source à température constante,
      
      
   4. d'associer directement les propriétés de l'aluminium.
      
      

   L'aide en ligne vous aidera à choisir les bons sous-modèles, en particulier les paramètres et les variables internes donnent beaucoup d'indications.
   
   

3. Définitions des paramètres numériques associés aux composants

   Voici les données physiques que vous devez traduire avec les paramètres composants:
   
   

   1. la barre mesure 1 mètre de long,
      
      
   2. elle à une section carrée de 0,1 mètre de coté,
      
      
   3. à l'instant initial, elle est à la température 15° en tout point,
      
      
   4. elle est entièrement en aluminium. Amesim contient un fichier de référence pour l'aluminium, si vous voulez le consulter rapidement, vous pouvez l'ouvrir en cliquant sur ce lien: pure_aluminum.data
      
      
   5. Elle est chauffée en une extrémité par une source de chaleur à température constante 40°C. Toutes les autres parois de la barre sont supposées adiabatiques.
      
      

   Remarques méthodologiques:
   
   Il est fortement recommandé de:
   
   

   • de créer des paramètres globaux qui pourront être utilisés dans tous les composants,
     
     
   • d'utiliser les paramètres globaux pour paramètrer le premier composant de chaque type,
     
     
   • de copier-coller les paramètres pour les fonctions qui ont des paramètres identiques.
     
     

4. Calculs et exploitation des résultats

   1. Estimez le temps pour atteindre le régime stationnaire du système.
      Rq: ce temps doit être de l'ordre de 20000 secondes
      
      
   2. Tracez la courbe de température de l'extrémité non chauffé de la barre en fonction du temps.
      
      
   3. En fait le nombre de tronçon est trop petit pour avoir une représentation précise du phénomène de conduction dans la barre.
      Sur le même espace de travail, recréez la même modélisation deux fois en discrétisant la barre respectivement en 4 et 10 éléments (on utilisera judicieusement les copiages/collages de composants ainsi que l'attribution de paramètres commun pour réaliser ce travail rapidement).
      
      
   4. Tracez sur un même graphique la température du bout de la barre en fonction du temps pour les trois discrétisations du système réalisées.
      
      
   5. Concluez par rapport à la méthode pour valider un choix de nombre de tronçons.
      
      
   6. Améliorez la présentation de votre tracé de courbes de températures (vous pourrez par exemple nommer l'axe des abscisses, renommez vos courbes etc...).
      Saississez dans votre fichier vos conclusions par rapport à la question précédente.
      
      
   7. Si on considère le même système mais avec comme matériau de l'or à la place de l'aluminium, déterminez le temps pour atteindre le régime stationnaire du système.
      Rq: ce temps doit être de l'ordre de 15000 secondes
      
      
   8. Une fois votre travail terminé, fermez votre fichier et purgez-le.