Nous avons vu précédemment le mode de régulation T.O.R. , le plus simple utilisé pour les systèmes thermiques. Lorsque l'on veut fixer plus précisément une grandeur physique on met en oeuvre des systèmes de régulation continus dans lesquels on module l'action de manière continue.

Dans cette activité nous allons voir comment régler la puissance de chauffage dans un four de manière à assurer une température constante dans celui-ci. Les régulateurs P.I.D. (proportionnel / intégrale / dérivé) sont parmi les plus utilisés industriellement pour cela, nous allons mettre en oeuvre un correcteur de ce type.

Régulateur de température PID

Cette activité consituera une introduction aux notions concernant les correcteurs, vous aurez plus tard l'occasion de les étudier de manière détaillée en cours d'automatique (EP4 second semestre).

 Travail à réaliser:

1. Téléchargez et ouvrez le fichier four_init.ame .
   Ce fichier représente de manière très simplifiée un four.
   Notez que dans cette modélisation le système de chauffage fournit une puissance à l'air à l'intérieur du four, l'état du capteur de température évoluant par échange convectif avec ce même air.
   Dans le fichier fourni la puissance du chauffage est indépendante de toute mesure, vous allez changer cela dans la suite du travail.
   
   
2. Insérez une fonction de signal constant représentant la température de consigne, on attribuera la valeur de 250°C. Essayez de proposer une boucle de régulation ajustant la puissance de chauffe de manière à ce que la température du capteur atteigne la température de consigne. Réaliser ce travail n'est pas facile, inutile d'y passer plus de 15 minutes si vous n'y arrivez pas, la suite du sujet donne une méthode pour le faire. Attention, il est attendu une régulation où la puissance varie en fonction des conditions de fonctionnement de manière à avoir un réponse rapide et stable, une régulation de type tout ou rien ne conviendra donc pas.
   
   
3. Insérez une boucle de régulation proportionnelle dans le système (voir cette copie d'écran à ce lien). Testez la régulation avec des valeurs du gain Kp égales à 1, 5, 10 et 100. Comparez les températures finales obtenues après stabilisation et les températures maximales atteintes par l'air pendant la régulation.
   
   
4. Pour Kp=5, tracez sur le même graphe la température de l'air et celle du capteur. Interprétez la différence, à votre avis est-ce que cela va avoir une influence sur la régulation ?
   
   
5. Déterminez le gain le plus élevé qui permet, au cours de la montée en température du four, de ne pas avoir un dépassement de la température de l'air par rapport à la température finale. On évaluera cette valeur avec une tolérance de 0,5.
   
   Pour tout la suite du travail vous conserverez ce gain pour l'action proportionnelle.
   
   
6. En fait ce type de régulation ne permet pas d'atteindre la valeur finale souhaitée, pour améliorer ça, on ajoute une correction égale à l'intégration de la différence entre la consigne et la mesure, c'est le I de P.I.D. . Modifiez votre circuit de manière à intégrer de terme correctif comme dans la copie d'écran disponible à ce lien.
   
   
7. Réglez le gain de la fonction intrégale à Ki=0,001 simulez et observez la température finale atteinte par l'air, comparez à l'évolution de la température sans correction intégrale.
   Tracez sur un même graphique la sortie de la fonction proportionnelle, de la fonction intégrale et de la somme des deux.
   
   
8. Pour Ki=1 et Ki=5 observez la stabilité de la régulation. Tracez la puissance délivrée par le système de chauffage à l'air. Observez qu'elle prend des valeurs peu réalistes car elle présente des puissances excessives dans ses plus hautes valeurs et des puissances négatives (refroidissement) difficile à réaliser techniquement pour un four.
   
   Ajoutez un composant de saturation SAT0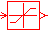 (sous-dossier discontinuities de la bibliothèque signal, Control) qui permet de limiter la puissance de chauffe entre 0W et 2kW et relancez les simulations pour voir l'impact.
   
   
9. Déterminez le gain de la fonction intégrale le plus élevé de manière à ce qu'au cours de la montée en température du four, la température de l'air ne dépasse pas de plus de 20°C la température finale. On évaluera la valeur avec une tolérance de 0,001.
   
   
10. Avec les valeurs de gains déterminés dans les questions précédentes, déterminez le temps pour que le système se stabilise à 250°C avec une tolérance de 0,5°C.
    
    
11. Nous allons maintenant simuler un fonctionnement à partir de l'état stationnaire, lorsque l'air dans le four est à 250°C. Modifiez la consigne en température de manière à la rendre variable et égale au signal dont le tracé est disponible à ce lien.
    Lancez une simulation temporelle en commençant à l'état d'équilibre, pour cela le plus simple est de lancer un calcul de type Stabilizing + Dynamic (sélectionnable dans l'onglet Standard options des paramètres de calcul). Tracez sur le même graphe la consigne et la température de l'air. Déterminez la différence maximum entre des deux valeurs au cours de ce cycle.
    
    
12. Une fois votre travail terminé, fermez votre fichier et purgez-le.
    
    

Quelques résultats:
Pour une boucle P, le gain maximum qui permet ne de pas avoir de dépassement est k=3.
Le gain du correcteur intégrale permettant de ne pas dépasser de plus de 20°C la température de consigne est de l'ordre de k=0,007.
Le temps pour arriver à une stabilisation à 250°C +-0,5°C est de l'ordre de 6125s.
Lors de l'évolution de consigne à partir d'un régime stabilisé, la différence maximum entre la température de consigne et la température de l'air est de 19,3°C.

Remarque:
L'ouvrage "Génie climatique et énergétique", de Jean-Baptiste Bouvenot et Bernard Flament, résume simplement l'influence des contributions des différentes fonctions des P.I.D. ainsi:

Action	Rapidité	Précision	Stabilité
P
I
D